Hallo,
ich entwickle im Moment eine GDI+ 3D-Engine.
Funktioniert _relativ gut, auch Clipping et cetera wurden bereits implementiert.
Der Ansatz für Clipping war folgender:
I.) Prüfe ob Vertex hinter der Kamera ist ( einfache Planar-Rechnungen, á la, wenn lambda negativ ist dann ja)
II.) wenn ja => ziehe von sichtbaren Vertizes eine Gerade zum unsichtbaren Vertex, bis Kollision mit Ebene.
wenn kollidiert, merke neue Vertex-Position, projiziere auf Bildschirm. Es entsteht nun ein Quadrangel, ( was logisch ist, schneidet man ein Dreieck an einer Ecke ab, erhält man ein Trapez)
II.) Wenn nein, alle drei Vertizes direkt projizieren.
Das Resultat ist dann exakt dasselbe wie bei MonoGame, je näher man ans Dreieck heranrückt, desto größer werden die Winkel zwischen den jeweiligen Vertizes.
Problem nun:
Die Engine soll _ Texturen auf Dreiecke mappen können.
Die Dreiecke, respektive die Polygone( man darf Sonderfall Trapez nicht vergessen), liegen projiziert vor.
Um Texturen auf Dreiecke mappen zu können greift man natürlich auf baryzentrische Koordinate zurück; geht auch sicherlich gut, bis eben der Spieler
zu nah an eine Ecke rückt, sodass ein Trapez zurückgegeben wird.
Für diesen Fall hab ich mir überlegt, beim Sonderfall Trapez einfach erneut zwei Geraden zu generieren( aber diesmal eben nicht im Raum, sondern Bildschirm-Koordinaten), und sie gleichzusetzen ( einfache lineare Algebra).
Code:
Funktioniert soweit gut bis obige Konsequenz ( je näher man ans Dreieck heranrückt, desto größer werden die Winkel zwischen den jeweiligen Vertizes) eintritt.
Wenn nämlich die Winkel zu groß werden, gehen die Geraden auseinander ( siehe Bilder unten), und schneiden sich dann im falschen ( eigentlich richtigen) Punkt.
Korrekte Darstellung ( das gefüllte Polygon ist das Trapez, die beiden Linien das fortzuführende Dreieck):
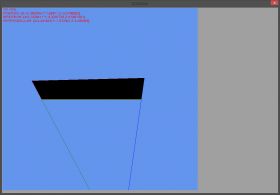
Inkorrekte Darstellung:
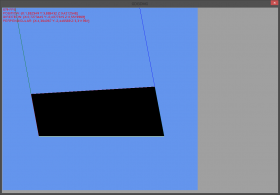
Besser erklärt durch folgende Situation:
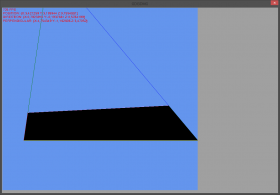
Die Winkel sind einfach so groß, das quasi die Vorzeichen sich ändern, und sich (bildschirmkoordinaten-technisch) im Negativen Bereich treffen.
Habe nach 3D-Baryzentrischen Koordinaten gesucht, aber nicht fündig geworden.
Wüsstet ihr eine Lösung?
Lieben Dank!
_
ich entwickle im Moment eine GDI+ 3D-Engine.
Funktioniert _relativ gut, auch Clipping et cetera wurden bereits implementiert.
Der Ansatz für Clipping war folgender:
I.) Prüfe ob Vertex hinter der Kamera ist ( einfache Planar-Rechnungen, á la, wenn lambda negativ ist dann ja)
II.) wenn ja => ziehe von sichtbaren Vertizes eine Gerade zum unsichtbaren Vertex, bis Kollision mit Ebene.
wenn kollidiert, merke neue Vertex-Position, projiziere auf Bildschirm. Es entsteht nun ein Quadrangel, ( was logisch ist, schneidet man ein Dreieck an einer Ecke ab, erhält man ein Trapez)
II.) Wenn nein, alle drei Vertizes direkt projizieren.
Das Resultat ist dann exakt dasselbe wie bei MonoGame, je näher man ans Dreieck heranrückt, desto größer werden die Winkel zwischen den jeweiligen Vertizes.
Problem nun:
Die Engine soll _ Texturen auf Dreiecke mappen können.
Die Dreiecke, respektive die Polygone( man darf Sonderfall Trapez nicht vergessen), liegen projiziert vor.
Um Texturen auf Dreiecke mappen zu können greift man natürlich auf baryzentrische Koordinate zurück; geht auch sicherlich gut, bis eben der Spieler
zu nah an eine Ecke rückt, sodass ein Trapez zurückgegeben wird.
Für diesen Fall hab ich mir überlegt, beim Sonderfall Trapez einfach erneut zwei Geraden zu generieren( aber diesmal eben nicht im Raum, sondern Bildschirm-Koordinaten), und sie gleichzusetzen ( einfache lineare Algebra).
Code:
C#-Quellcode
- public float Slope { get; private set; }
- public float YIntersection { get; private set; }
- public AlgebraicRay(Vector2 a, Vector2 b)
- {
- float dx = b.X - a.X;
- float dy = b.Y - a.Y;
- Slope = dy / dx;
- YIntersection = a.Y - Slope * a.X;
- }
- public float f(float x)
- {
- return Slope * x + YIntersection;
- }
- public Vector2 Intersects(AlgebraicRay a)
- {
- /*
- *
- * mx+b=mx+b
- */
- float m0 = Slope;
- float m1 = a.Slope;
- float b0 = YIntersection;
- float b1 = a.YIntersection;
- float rM = m1 - m0;
- float rB = b0 - b1;
- float x = rB / rM;
- return new Vector2(x, f(x));
- }
Funktioniert soweit gut bis obige Konsequenz ( je näher man ans Dreieck heranrückt, desto größer werden die Winkel zwischen den jeweiligen Vertizes) eintritt.
Wenn nämlich die Winkel zu groß werden, gehen die Geraden auseinander ( siehe Bilder unten), und schneiden sich dann im falschen ( eigentlich richtigen) Punkt.
Korrekte Darstellung ( das gefüllte Polygon ist das Trapez, die beiden Linien das fortzuführende Dreieck):
Inkorrekte Darstellung:
Besser erklärt durch folgende Situation:
Die Winkel sind einfach so groß, das quasi die Vorzeichen sich ändern, und sich (bildschirmkoordinaten-technisch) im Negativen Bereich treffen.
Habe nach 3D-Baryzentrischen Koordinaten gesucht, aber nicht fündig geworden.
Wüsstet ihr eine Lösung?
Lieben Dank!
_
Und Gott alleine weiß alles am allerbesten und besser.
Dieser Beitrag wurde bereits 2 mal editiert, zuletzt von „φConst“ ()




